Simulink 2阶系统模拟
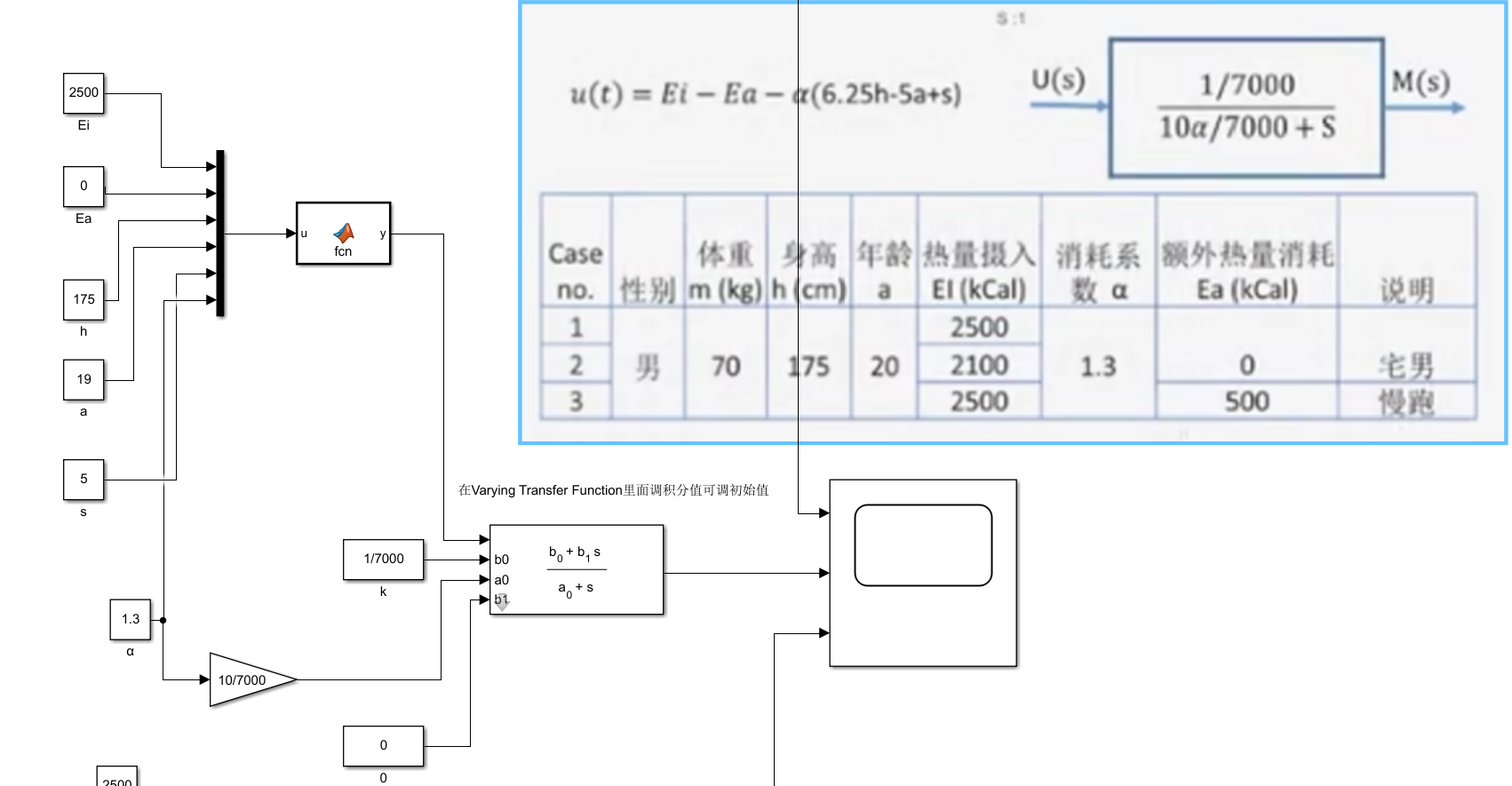
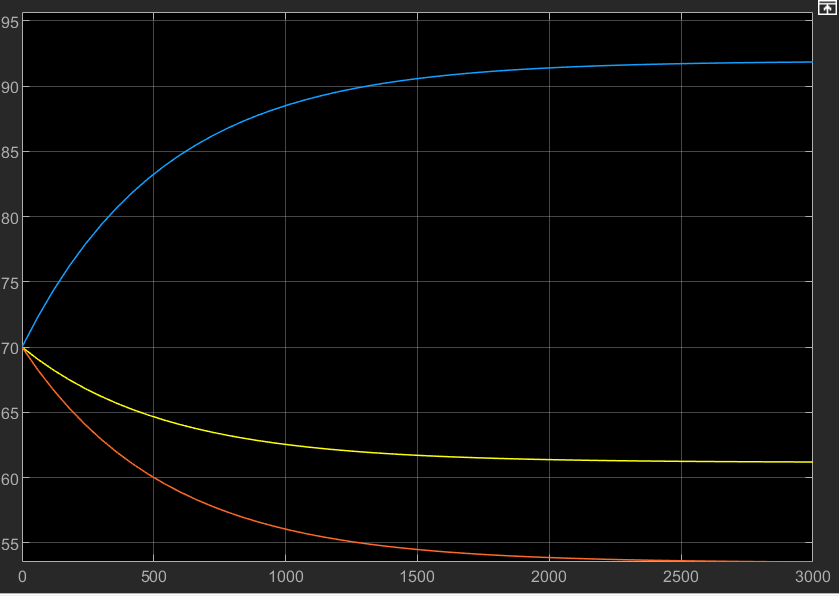
减肥模型
在Varying Transfer Function里面调积分值可调初始值
P控制
这个模型里是不是可以把这个Kp看成一个“决心因子”或者“自控因子”，Kp越大，表示你减小差距的愿望越强烈，采取的行动越多。根据系统的根我们知道Kp+10α两个参数共同影响着体重的输出结果。
Kp>-13时是当你的决心Kp在代谢率系数10α的承受范围内，，体重总是可控的，而且愿望越强烈，就能越快达到目标。Kp>0说明你比较节制，只要体重超过预期，就会采取行动减肥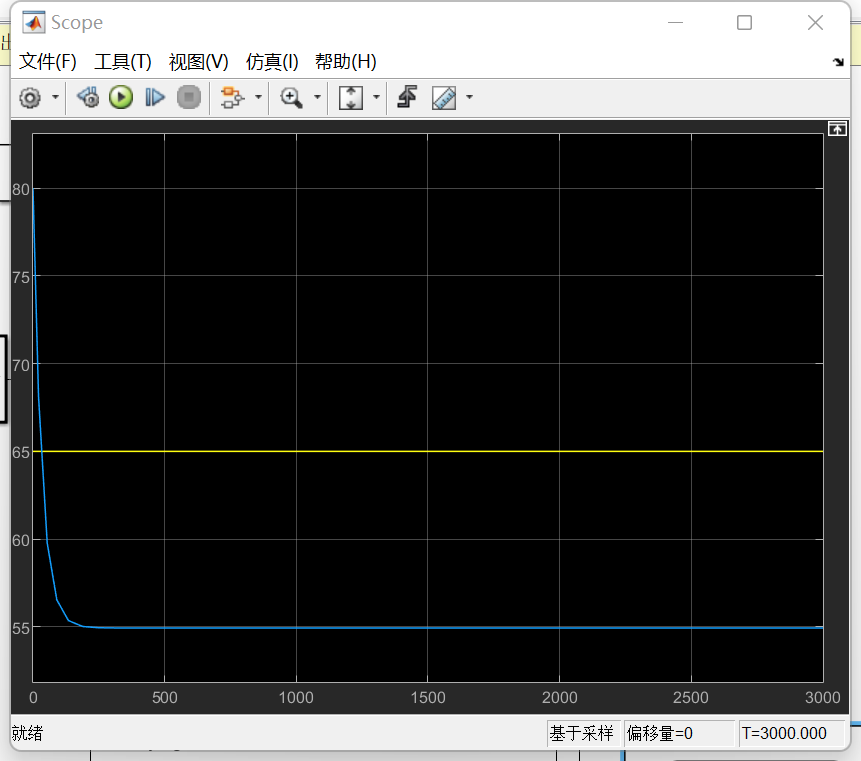
；Kp=0说明you just dont care，不会因为体重和预期有差距而产生任何行动，任由干扰项身体代谢率 do the jobKp<0（比如-5）说明你就算体重超过预期仍然快乐养膘，这时只要你的快乐程度没有战胜基础代谢率（系统自身的稳定性储备），那么体重虽然慢但仍然早晚可以依靠自然代谢率降下来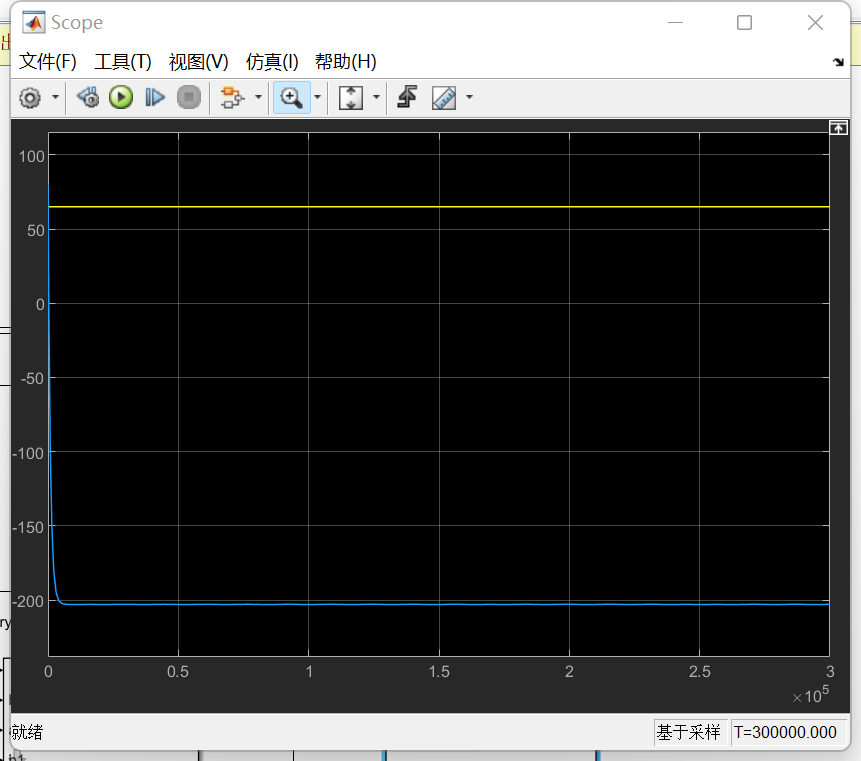
Kp<-13，身体代谢率也救不了你的时候，你的体重就会疯狂爆炸。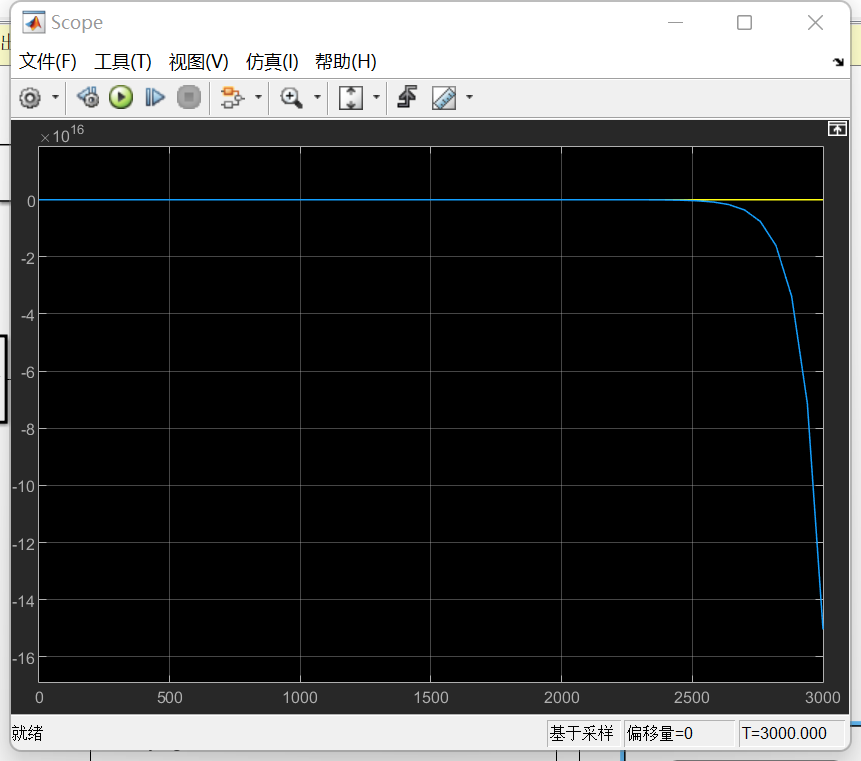
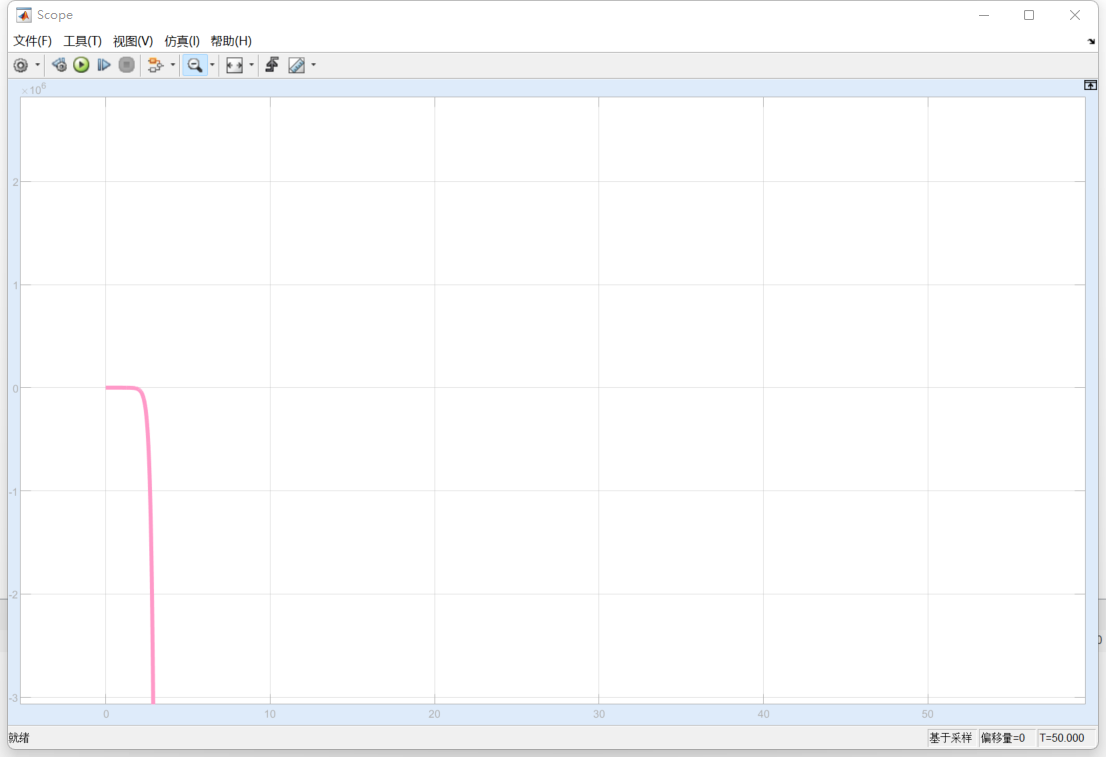
会发现仍存在steady state error
PI 控制
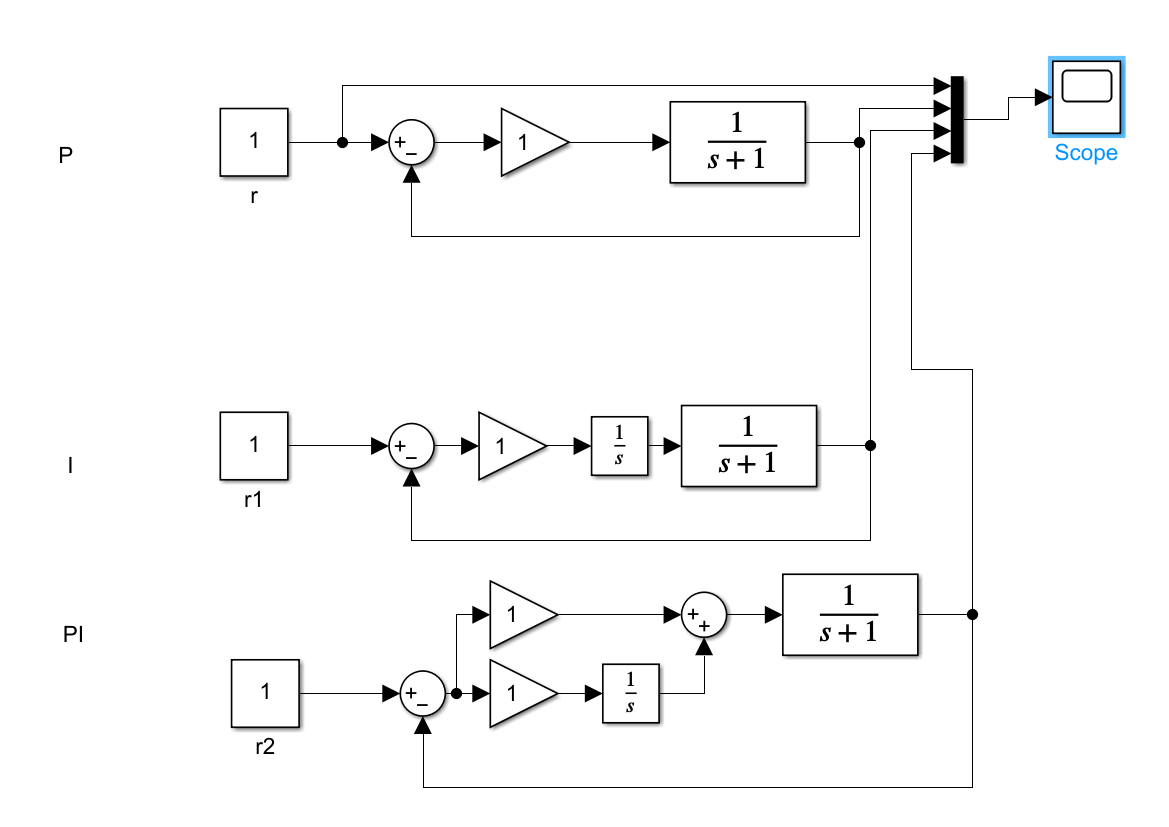
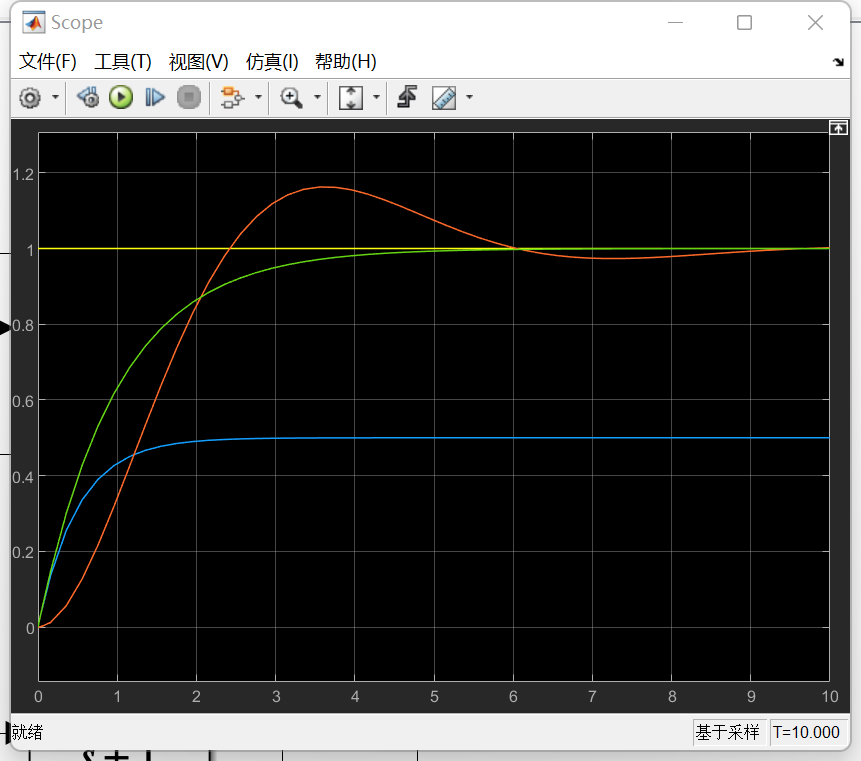
Simulink 2阶系统模拟
\[F=ma\]
Vibration 振动
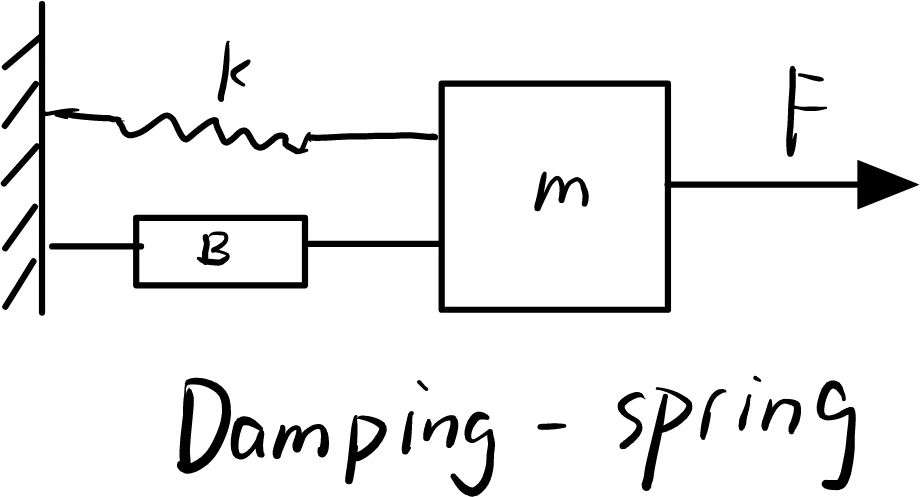
\[\ddot x+\frac{B}{m}\dot x+\frac{k}{m}x=F\] \[ \left\{ \begin{aligned} &\text{Natural Frequency}&\omega_n & = \sqrt{\frac{k}{m}} \\ &\text{Damping ratio}&\zeta & = \frac{B}{\sqrt{2km}} \\ \end{aligned} \right. \] \[ \text{Initial condition}\left\{ \begin{aligned} &F=0\\ &x(0)=x_0\\ &\dot x(0)=\dot x_0 \end{aligned} \right. \]
得到： \[\ddot x+2\zeta\omega_n \dot x+\omega_n^2x=0\]
characteristic equation 特征方程： \[x^2+2\zeta\omega_n \dot x+\omega_n^2x=0\] $$ { \[\begin{aligned} &x_1=-\zeta\omega_n+\omega_n \sqrt{\zeta^2-1}\\ &x_2=-\zeta\omega_n-\omega_n \sqrt{\zeta^2-1}\\ \end{aligned}\]. $$
Simulink
\[ \text{setting}\left\{
\begin{aligned}
&\ddot x=-2\zeta\omega_n \dot x-\omega_n^2x\\
&x(0)=5\\
&\dot x(0)=0
\end{aligned}
\right.
\] 
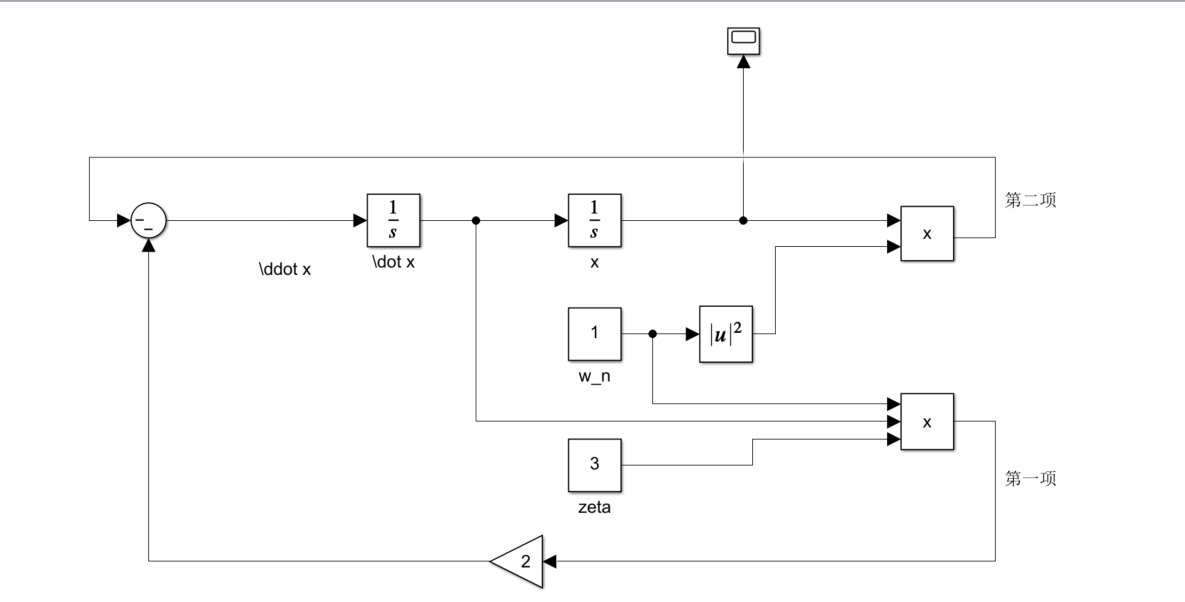# 不同\(\zeta\)下的响应曲线
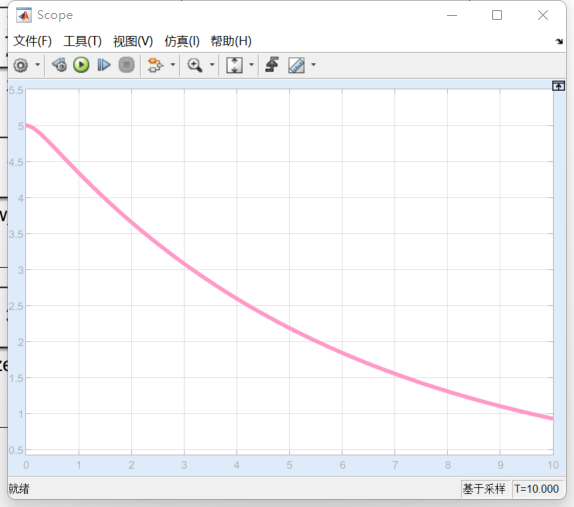
over damped
\(\zeta>1\) 即 \(\frac{B}{\sqrt{2km}}>1\).
两实根\(X(t)=C_1e^{\lambda_1t}+C_2e^{\lambda_2t}\)
收敛取决于\(\lambda_1\)，因为\(\left|\lambda_1\right|\)更小
critical damped
\(\zeta=1\) 即 \(\frac{B}{\sqrt{2km}}=1\).
一实根 \(X(t)=(C_1+C_2t)e^{\lambda
t}\)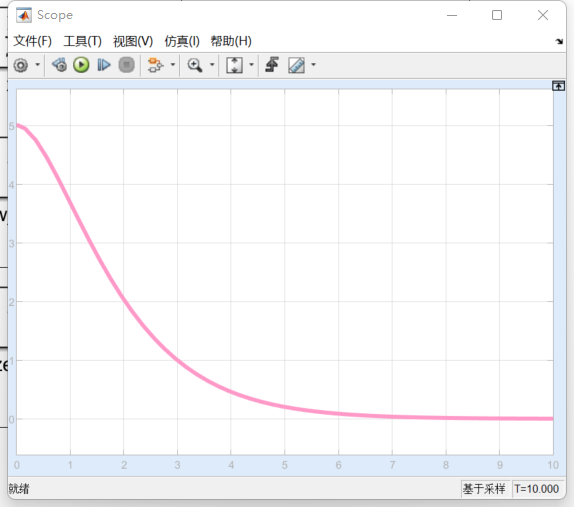 
3. under damped
\(\zeta<1\) 即 \(\frac{B}{\sqrt{2km}}<1\).
一对复共轭根\(\lambda=\alpha \pm i\beta\)
\(X(t)=e^{-\alpha t}(C_1\cos\beta t+C_2\sin
\beta t)\)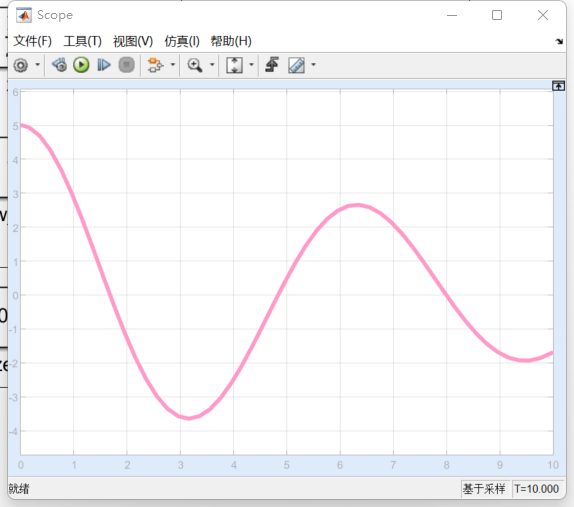 
4. 3中\(\alpha=0\)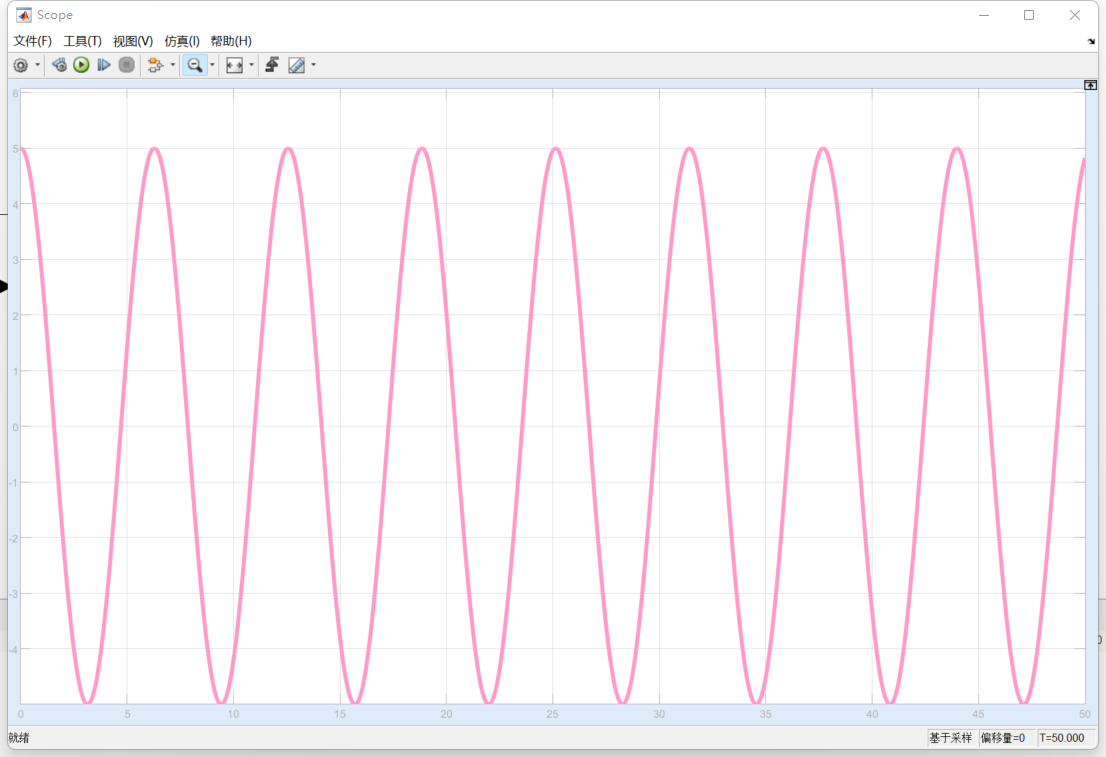 
- \(-1<\zeta<0\) 即 -1<\(\frac{B}{\sqrt{2km}}<0\).
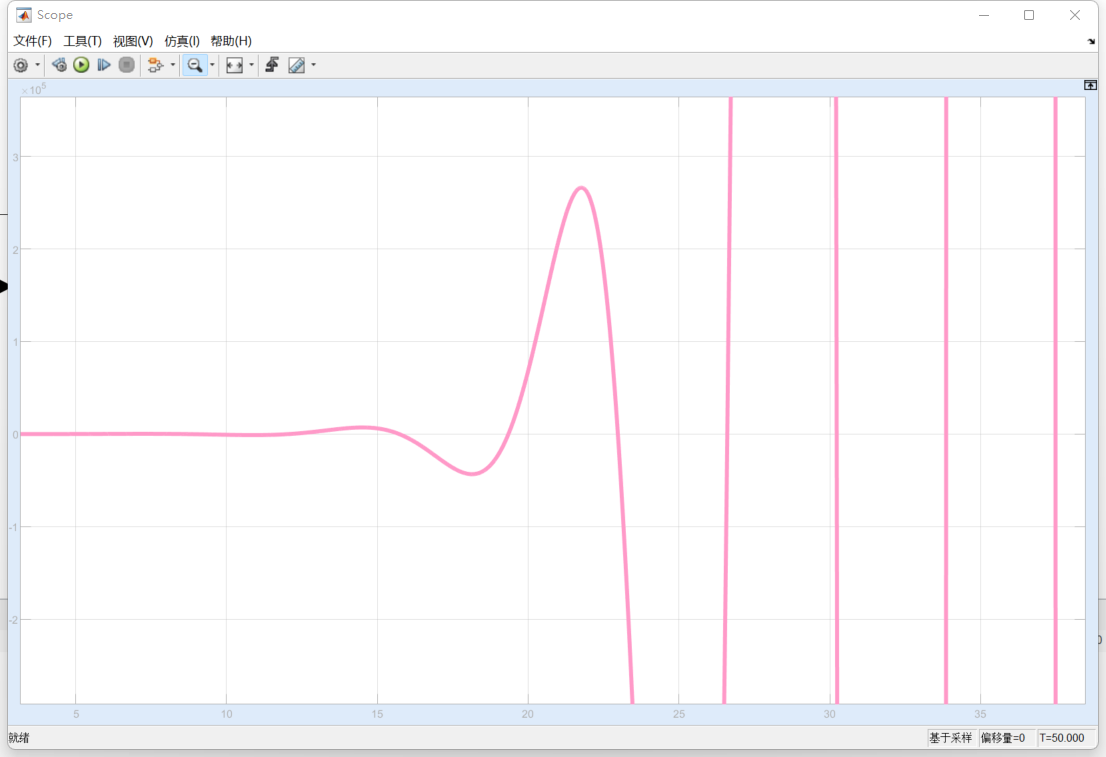
- \(\zeta<-1\) 即 -1<\(\frac{B}{\sqrt{2km}}<-1\).
