神经网络基础
1 | |
其中net(X)是net.__call__(X)的简写。
1 | |
通常,我们利用GPU并行运算的优势,处理合理大小的“小批量”。 每个样本都可以并行地进行模型计算,且每个样本损失函数的梯度也可以被并行计算。 GPU可以在处理几百个样本时,所花费的时间不比处理一个样本时多太多。
Softmax分类任务里分类精度
注意==对数据类型敏感 1
2
3
4
5
6def accuracy(y_hat, y): #@save
"""计算预测正确的数量"""
if len(y_hat.shape) > 1 and y_hat.shape[1] > 1:
y_hat = y_hat.argmax(axis=1)
cmp = y_hat.type(y.dtype) == y
return float(cmp.type(y.dtype).sum())data_iter读取数据集
这里定义一个实用程序类Accumulator,用于对多个变量进行累加。
在上面的evaluate_accuracy函数中,
我们在(Accumulator实例中创建了2个变量,
分别用于存储正确预测的数量和预测的总数量)。
当我们遍历数据集时,两者都将随着时间的推移而累加。
1
2
3
4
5
6
7
8
9
10
11
12
13class Accumulator: #@save
"""在n个变量上累加"""
def __init__(self, n):
self.data = [0.0] * n
def add(self, *args):
self.data = [a + float(b) for a, b in zip(self.data, args)]
def reset(self):
self.data = [0.0] * len(self.data)
def __getitem__(self, idx):
return self.data[idx]
1 | |
神经网络基础
块
要想直观地了解块是如何工作的,最简单的方法就是自己实现一个。 在实现我们自定义块之前,我们简要总结一下每个块必须提供的基本功能: 1. 将输入数据作为其前向传播函数的参数。
通过前向传播函数来生成输出。请注意,输出的形状可能与输入的形状不同。例如,我们上面模型中的第一个全连接的层接收一个20维的输入,但是返回一个维度为256的输出。
计算其输出关于输入的梯度,可通过其反向传播函数进行访问。通常这是自动发生的。
存储和访问前向传播计算所需的参数。
根据需要初始化模型参数。
从零开始编写一个块
包含一个多层感知机,其具有256个隐藏单元的隐藏层和一个10维输出层。
1
2
3
4
5
6
7
8
9
10
11
12
13# 用模型参数声明层。这里,我们声明两个全连接的层
class MLP(nn.Module):# 继承了块的定义
def __init__(self):
# 在类实例化时也可以指定其他函数参数,例如模型参数params(稍后将介绍)
super().__init__()#调用MLP的父类Module的构造函数来执行必要的初始化。
self.hidden = nn.Linear(20, 256) # 隐藏层
self.out = nn.Linear(256, 10) # 输出层
# 定义模型的前向传播,即如何根据输入X返回所需的模型输出
def forward(self, X):
# 注意,这里我们使用ReLU的函数版本,其在nn.functional模块中定义。
return self.out(F.relu(self.hidden(X)))
块的一个主要优点是它的多功能性。 我们可以子类化块以创建层(如全连接层的类)、 整个模型(如上面的MLP类)或具有中等复杂度的各种组件。 我们在接下来的章节中充分利用了这种多功能性, 比如在处理卷积神经网络时。
顺序块
要编写简化的MySequential只需定义好: 1.
将块逐个追加到列表中的函数;
- 前向传播函数,用于将输入按追加块的顺序传递给块组成的“链条”。
1
2
3
4
5
6
7
8
9
10
11
12
13class MySequential(nn.Module):
def __init__(self, *args):
super().__init__()
for idx, module in enumerate(args):# 传入要用的层
# 这里,module是Module子类的一个实例。我们把它保存在'Module'类的成员
# 变量_modules中。_module的类型是OrderedDict
self._modules[str(idx)] = module
def forward(self, X):
# OrderedDict保证了按照成员添加的顺序遍历它们
for block in self._modules.values():
X = block(X)
return X
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
简而言之,```_modules```的主要优点是: 在模块的参数初始化过程中, 系统知道在```_modules```字典中**查找需要初始化参数**的子块。
## 执行更灵活的代码
如控制流或数学运算
例如,我们需要一个计算函数$f(\mathbf x,\mathbf w)=c\cdot \mathbf w^T\mathbf x$的层, 其中$\mathbf x$是输入, $\mathbf w$是参数, $c$是某个在优化过程中没有更新的指定常量。 因此我们实现了一个```FixedHiddenMLP```类,如下所示:
```python
class FixedHiddenMLP(nn.Module):
def __init__(self):
super().__init__()
# 不计算梯度的随机权重参数c。因此其在训练期间保持不变
self.rand_weight = torch.rand((20, 20), requires_grad=False)
self.linear = nn.Linear(20, 20)
def forward(self, X):
X = self.linear(X)
# 使用创建的常量参数以及relu和mm函数
X = F.relu(torch.mm(X, self.rand_weight) + 1)
# 复用全连接层。这相当于两个全连接层共享参数
X = self.linear(X)
# 控制流,缩小输出
while X.abs().sum() > 1:
X /= 2
return X.sum()
混合嵌套块
1 | |
Q
如果将MySequential中存储块的方式更改为Python列表,会出现什么样的问题?
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30class MySequential2(nn.Module):
"""顺序块"""
# 使用list
def __init__(self, *args):
super(MySequential2, self).__init__()
self.sequential = []
for module in args:
self.sequential.append(module)
def forward(self, X):
# OrderedDict保证了按照成员添加的顺序遍历它们
for module in self.sequential:
X = module(X)
return X
linear1 = nn.Linear(20, 256)
relu = nn.ReLU()
linear2 = nn.Linear(256, 10)
net = MySequential(linear1, relu, linear2)
net2 = MySequential2(linear1, relu, linear2)
# 结果一样
# print(net(X))
# print(net2(X))
# 使用_modules方便打印net的网络结构和参数,而list则无法做到
# print(net, '\n', net.state_dict())
# print(net2, '\n', net2.state_dict())实现一个块,它以两个块为参数,例如net1和net2,并返回前向传播中两个网络的串联输出。这也被称为平行块。
## 参数管理1
2
3
4
5
6
7
8
9
10
11
12
13
14class MyBlock(nn.Module):
def __init__(self, block1, block2):
super(MyBlock, self).__init__()
self.block1 = block1
self.block2 = block2
def forward(self, X):
X = torch.cat((self.block1(X), self.block2(X)), 1)
return X
block = MyBlock(nn.Linear(20, 5), nn.Linear(20, 5))
net = nn.Sequential(block, nn.ReLU(), nn.Linear(10, 5))
print(net(X).shape)访问参数,用于调试、诊断和可视化;
参数初始化;
在不同模型组件间共享参数。
我们首先看一下具有单隐藏层的多层感知机: 1
2
3
4
5
6import torch
from torch import nn
net = nn.Sequential(nn.Linear(4, 8), nn.ReLU(), nn.Linear(8, 1))
X = torch.rand(size=(2, 4))
net(X)1
2tensor([[-0.0619],
[-0.0489]], grad_fn=<AddmmBackward0>)
1 | |
1 | |
参数类
注意,每个参数都表示为参数类的一个实例.
1
2
3print(type(net[2].bias))
print(net[2].bias)
print(net[2].bias.data)1
2
3
4<class 'torch.nn.parameter.Parameter'>
Parameter containing:
tensor([-0.0291], requires_grad=True)
tensor([-0.0291])1
2net[2].weight.grad == None #True1
2print(*[(name, param.shape) for name, param in net[0].named_parameters()])
print(*[(name, param.shape) for name, param in net.named_parameters()])1
2
3('weight', torch.Size([8, 4])) ('bias', torch.Size([8]))
('0.weight', torch.Size([8, 4])) ('0.bias', torch.Size([8])) ('2.weight', torch.Size([1, 8])) ('2.bias', torch.Size([1]))
#1层是偏置,没有权重1
2
3
4
5
6
7
8
9
10
11
12
13def block1():
return nn.Sequential(nn.Linear(4, 8), nn.ReLU(),
nn.Linear(8, 4), nn.ReLU())
def block2():
net = nn.Sequential()
for i in range(4):
# 在这里嵌套
net.add_module(f'block {i}', block1())
return net
rgnet = nn.Sequential(block2(), nn.Linear(4, 1))
rgnet(X)
1 | |
1 | |
参数初始化
1 | |
1 | |
自定义初始化
1 | |
参数绑定
1 | |
好处:
共享参数通常可以节省内存,并在以下方面具有特定的好处:
- 对于图像识别中的CNN,共享参数使网络能够在图像中的任何地方而不是仅在某个区域中查找给定的功能。
- 对于RNN,它在序列的各个时间步之间共享参数,因此可以很好地推广到不同序列长度的示例。
- 对于自动编码器,编码器和解码器共享参数。 在具有线性激活的单层自动编码器中,共享权重会在权重矩阵的不同隐藏层之间强制正交。
延后初始化
我们定义了网络架构,但没有指定输入维度。
我们添加层时没有指定前一层的输出维度。
我们在初始化参数时,甚至没有足够的信息来确定模型应该包含多少参数。
有些读者可能会对我们的代码能运行感到惊讶。 毕竟,深度学习框架无法判断网络的输入维度是什么。 这里的诀窍是框架的延后初始化(defers initialization), 即直到数据第一次通过模型传递时,框架才会动态地推断出每个层的大小。
在以后,当使用卷积神经网络时,
由于输入维度(即图像的分辨率)将影响每个后续层的维数,
有了该技术将更加方便。
现在我们在编写代码时无须知道维度是什么就可以设置参数,
这种能力可以大大简化定义和修改模型的任务。
接下来,我们将更深入地研究初始化机制。 1
2
3
4
5
6
7
8
9
10
11import torch
from torch import nn
"""延后初始化"""
net = nn.Sequential(nn.LazyLinear(256), nn.ReLU(), nn.LazyLinear(10))
print(net[0].weight) # 尚未初始化
print(net)
X = torch.rand(2, 20)
net(X)
print(net)
自定义层
和自定义网络差不多,都是Module的子类
什么参数都没有的层
1 | |
现在,我们可以将我们自定义的层作为组件合并到模型中 1
2
3
4net = nn.Sequential(nn.Linear(8, 128), CenteredLayer())
Y = net(torch.rand(4, 8))
Y.mean()
# tensor(-1.3970e-09, grad_fn=<MeanBackward0>)1
2
3
4
5
6
7
8class MyLinear(nn.Module):
def __init__(self, in_units, units):
super().__init__()
self.weight = nn.Parameter(torch.randn(in_units, units))#输入输出维度
self.bias = nn.Parameter(torch.randn(units,))
def forward(self, X):
linear = torch.matmul(X, self.weight.data) + self.bias.data
return F.relu(linear)#和之前不同,直接把relu做好1
2
3
4
5
6
7
8
9import torch
from torch import nn
from torch.nn import functional as F
x = torch.arange(4)
torch.save(x, 'x-file')
x2 = torch.load('x-file')
x2
pytorch只需要记录模型所有参数即可
1 | |
\(L_2\)正则 vs \(L_1\)正则
为什么我们首先使用范数\(L_2\),而不是范数\(L_1\)。 事实上,这个选择在整个统计领域中都是有效的和受欢迎的。 \(L_2\)正则化线性模型构成经典的岭回归(ridge regression)算法,\(L_1\) 正则化线性回归是统计学中类似的基本模型, 通常被称为套索回归(lasso regression)。 使用范数\(L_2\)的一个原因是它对权重向量的大分量施加了巨大的惩罚。 这使得我们的学习算法偏向于在大量特征上均匀分布权重的模型。 在实践中,这可能使它们对单个变量中的观测误差更为稳定。
相比之下,\(L_1\)惩罚会导致模型将权重集中在一小部分特征上, 而将其他权重清除为零。 这称为特征选择(feature selection),这可能是其他场景下需要的。
数据操作
大小
1
x.shape1
x.numel()1
2
3X = torch.arange(12, dtype=torch.float32).reshape((3,4))
Y = torch.tensor([[2.0, 1, 4, 3], [1, 2, 3, 4], [4, 3, 2, 1]])
torch.cat((X, Y), dim=0), torch.cat((X, Y), dim=1)1
2
3
4
5
6
7
8
9(tensor([[ 0., 1., 2., 3.],
[ 4., 5., 6., 7.],
[ 8., 9., 10., 11.],
[ 2., 1., 4., 3.],
[ 1., 2., 3., 4.],
[ 4., 3., 2., 1.]]),
tensor([[ 0., 1., 2., 3., 2., 1., 4., 3.],
[ 4., 5., 6., 7., 1., 2., 3., 4.],
[ 8., 9., 10., 11., 4., 3., 2., 1.]]))
1 | |
读取数据集
1 | |
1 | |
处理缺失值
1 | |
独热编码 one-hot encoding
1 | |
1 | |
单列的文本数据变成了两个特征
不建议深究传值还是传引用
生成器
生成器用了yield
| ## str和repr str和repr |
## 异常 try和except |
raise,finally |
| # 文件 |
| ## 打开 |
with open ('a.text','w') as f: |
| ## 读写 |
| ## 关闭 |
修饰器
加了帽子加了鞋垫
输入func
1 | |
实用性
- 函数运行的时间
TCP/IP协议
- 传输层 TCP
- 网络层 IP
三次握手
另一种 UDP
一次握手
get and post
- 明文和加密
json
轻量级的数据交换格式
java和JavaScript没啥关系
Vue封装了css,JavaScript,html
Beautifulsoap
能解析html里的数据的python库
Flask
SQL
关系型数据库
git
kaggle
Kaggle房价预测
下载
用到了下文定义的脚本 1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20# 如果没有安装pandas,请取消下一行的注释
# !pip install pandas
%matplotlib inline
import numpy as np
import pandas as pd
import torch
from torch import nn
from d2l import torch as d2l
DATA_HUB['kaggle_house_train'] = ( #@save
DATA_URL + 'kaggle_house_pred_train.csv',
'585e9cc93e70b39160e7921475f9bcd7d31219ce')
DATA_HUB['kaggle_house_test'] = ( #@save
DATA_URL + 'kaggle_house_pred_test.csv',
'fa19780a7b011d9b009e8bff8e99922a8ee2eb90')
train_data = pd.read_csv(download('kaggle_house_train'))
test_data = pd.read_csv(download('kaggle_house_test'))1
2print(train_data.shape)
print(test_data.shape)
(1460, 81)
(1459, 80) 1
2#前四个和最后两个特征以及标签
print(train_data.iloc[0:4, [0, 1, 2, 3, -3, -2, -1]])
预处理
我们可以看到,(在每个样本中,第一个特征是ID,)
这有助于模型识别每个训练样本。
虽然这很方便,但它不携带任何用于预测的信息。
因此,在将数据提供给模型之前,(我们将其从数据集中删除)。
1
all_features = pd.concat((train_data.iloc[:, 1:-1], test_data.iloc[:, 1:]))
提交
将预测保存在CSV文件中可以简化将结果上传到Kaggle的过程。
1
2
3
4
5
6
7
8
9
10
11
12
13
14def train_and_pred(train_features, test_features, train_labels, test_data,
num_epochs, lr, weight_decay, batch_size):
net = get_net()
train_ls, _ = train(net, train_features, train_labels, None, None,
num_epochs, lr, weight_decay, batch_size)
d2l.plot(np.arange(1, num_epochs + 1), [train_ls], xlabel='epoch',
ylabel='log rmse', xlim=[1, num_epochs], yscale='log')
print(f'训练log rmse:{float(train_ls[-1]):f}')
# 将网络应用于测试集。
preds = net(test_features).detach().numpy()
# 将其重新格式化以导出到Kaggle
test_data['SalePrice'] = pd.Series(preds.reshape(1, -1)[0])
submission = pd.concat([test_data['Id'], test_data['SalePrice']], axis=1)
submission.to_csv('submission.csv', index=False)
数据下载
下载
在整本书中,我们将下载不同的数据集,并训练和测试模型。
这里我们(实现几个函数来方便下载数据)。
首先,我们建立字典DATA_HUB,
它可以将数据集名称的字符串映射到数据集相关的二元组上,
这个二元组包含数据集的url和验证文件完整性的sha-1密钥。
所有类似的数据集都托管在地址为DATA_URL的站点上。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33import hashlib
import os
import tarfile
import zipfile
import requests
#@save
DATA_HUB = dict()
DATA_URL = 'http://d2l-data.s3-accelerate.amazonaws.com/'
# --------------------------
def download(name, cache_dir=os.path.join('..', 'data')): #@save
"""下载一个DATA_HUB中的文件,返回本地文件名"""
assert name in DATA_HUB, f"{name} 不存在于 {DATA_HUB}"
url, sha1_hash = DATA_HUB[name]
os.makedirs(cache_dir, exist_ok=True)
fname = os.path.join(cache_dir, url.split('/')[-1])
if os.path.exists(fname):
sha1 = hashlib.sha1()
with open(fname, 'rb') as f:
while True:
data = f.read(1048576)
if not data:
break
sha1.update(data)
if sha1.hexdigest() == sha1_hash:
return fname # 命中缓存
print(f'正在从{url}下载{fname}...')
r = requests.get(url, stream=True, verify=True)
with open(fname, 'wb') as f:
f.write(r.content)
return fname1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18def download_extract(name, folder=None): #@save
"""下载并解压zip/tar文件"""
fname = download(name)
base_dir = os.path.dirname(fname)
data_dir, ext = os.path.splitext(fname)
if ext == '.zip':
fp = zipfile.ZipFile(fname, 'r')
elif ext in ('.tar', '.gz'):
fp = tarfile.open(fname, 'r')
else:
assert False, '只有zip/tar文件可以被解压缩'
fp.extractall(base_dir)
return os.path.join(base_dir, folder) if folder else data_dir
def download_all(): #@save
"""下载DATA_HUB中的所有文件"""
for name in DATA_HUB:
download(name)
AutoML
1 | |
Spiking Neural Network 第三代神经网路
脉冲神经元
- ANN:直接过激活函数
- SNN:不断积累,过阈值之后再输出,然后重置。
- LIF
- IF
常被简化成离散计算 不是每时每刻都发放脉冲 ## 低功耗 - ANN:精度高但是功耗大 - SNN:基于事件触发的特性与神经形态的硬件(TrueNorth、SpiNNaker等)结合,极大降低功耗。如果用GPU、华为昇騰等则不行,功耗会更大。
鲁棒性
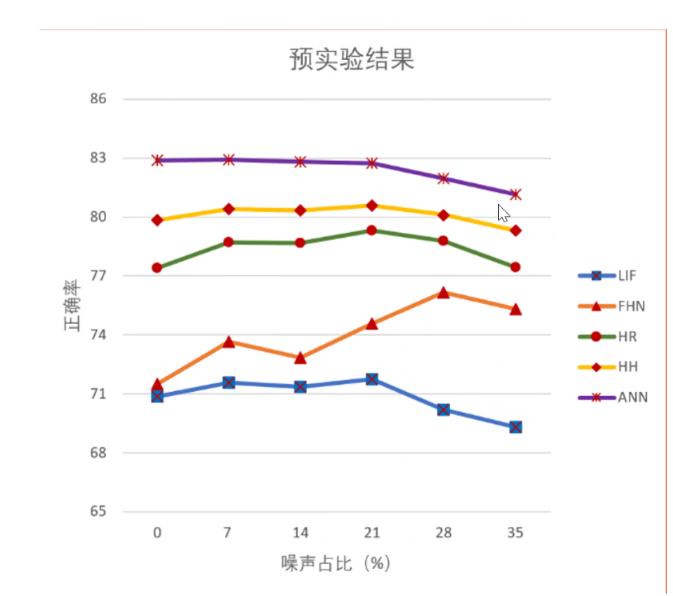 Why
积分带有高频滤波的特性 ## 学习方法 - 有监督 - Surrogate
Gradient Method(替代梯度 - Time-based Method - BP with
STDP(生物合理性)
Why
积分带有高频滤波的特性 ## 学习方法 - 有监督 - Surrogate
Gradient Method(替代梯度 - Time-based Method - BP with
STDP(生物合理性)
- 无监督
- Spike-based EM
- 奖励学习
- ANN-SNN
替代梯度
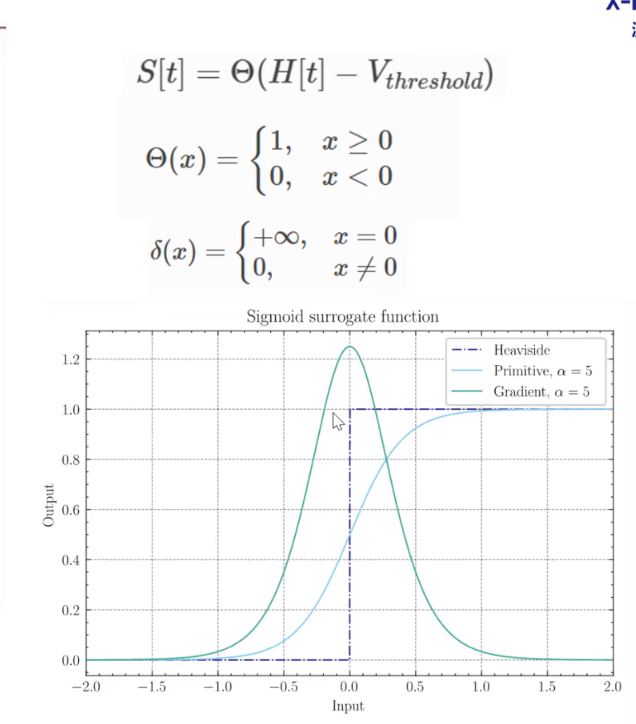 ## 总结 - 更具生物合理性 - 鲁棒性高 - 容易生物交叉 -
缺乏合适的类脑数据集、算法 - 性能不足,商业化低 - 脑科学认知不足 ##
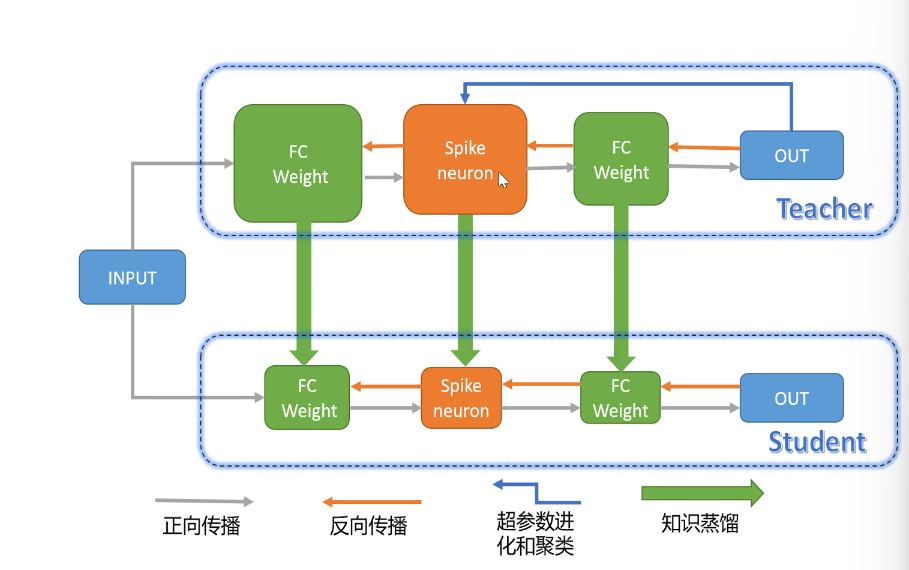
超参数进化和蒸馏 现有通用结构:单一神经元,生物仿生性差;
高维神经元:性能越来越好,鲁棒性越来越好
## 总结 - 更具生物合理性 - 鲁棒性高 - 容易生物交叉 -
缺乏合适的类脑数据集、算法 - 性能不足,商业化低 - 脑科学认知不足 ##
超参数进化和蒸馏 现有通用结构:单一神经元,生物仿生性差;
高维神经元:性能越来越好,鲁棒性越来越好 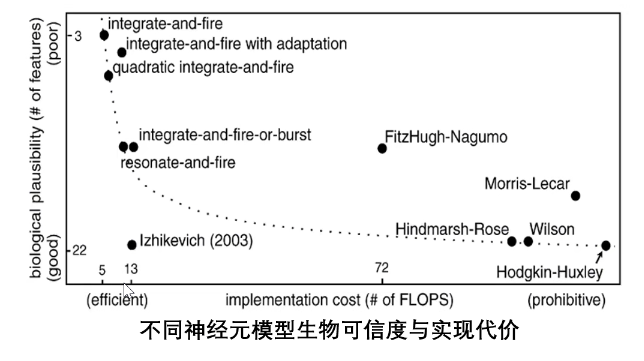 - 超参数过多 ,解决方法: 进化
- 计算代价大 ,解决方法: 蒸馏
- 超参数过多 ,解决方法: 进化
- 计算代价大 ,解决方法: 蒸馏
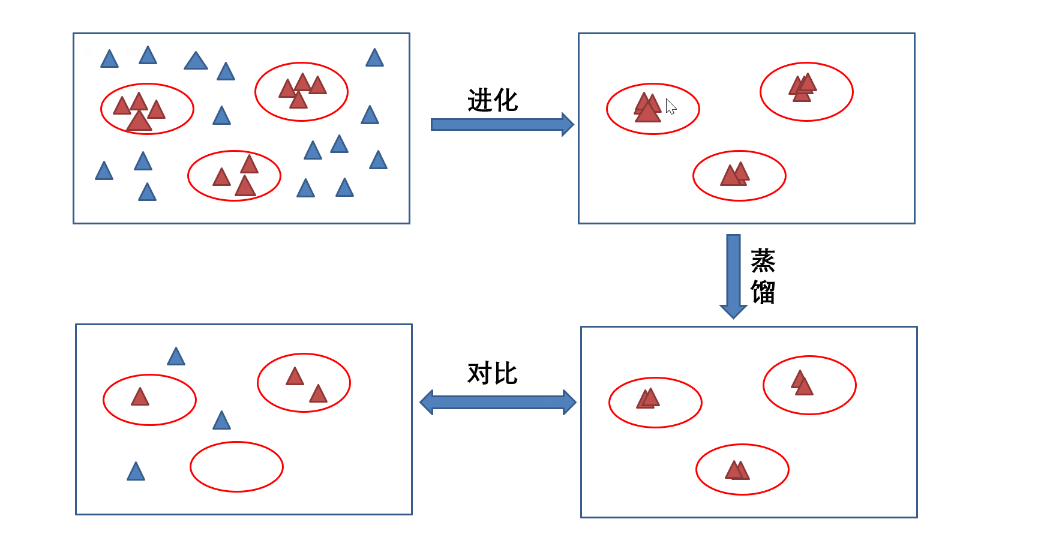
Transformer
Attention is all you need
多头注意力
前馈神经网络FFN
masked 多头注意力 遮住后来的信息
自注意力
并行化
没有循环结构
预训练
以前都是RNN
- 可用于图像处理
- 医学成像
- 语音识别
从NLP出发,拓展到多领域
计算机视觉
视频预测VFFP
- 双流计算
- 中间转换
计算量大
 ## 相关网站
## 相关网站