材力-公式篇
\(\frac{1}{\rho}=\frac{M}{EI}\)
主应力:\(\sigma=\frac{My}{I_z}\)
切应力:\(\tau=\frac{F_s S_z^*}{b I_z}\)
- 矩形:\(\tau=\frac{3}{2}\frac{F_s}{bh}\);
- 圆形:\(\tau=\frac{4}{3}\frac{F_s}{A}\);
- 圆筒:\(\tau=2\frac{F_s}{A},A=2\pi r\delta_0\);
截面几何性质(Properties of plane areas)
静矩和形心(The first moments of area & Centroid of an area)
极惯性矩 惯性矩 惯性积(Polar moment of inertia Moment of inertia Product of inertia)
平行移轴公式(Parallel-Axis theorem)
常用
- 圆
\[\begin{align} I_{\rho}&=\frac{\pi d^4}{32}=\frac{\pi r^4}{2}\\ I_{z}&=\frac{\pi d^4}{64}=\frac{\pi r^4}{4}\\ W&=\frac{i}{y_{max}} \end{align}\]
- 矩形 \[\begin{align} I_{z}=\frac{bh^3}{12}\\ W=\frac{bh^2}{6} \end{align}\]
转动相关
转轴公式(Rotation of axes)
方向:逆时针转为正
\[\begin{align} I_y'&=\frac{I_y+I_z}{2}+\frac{I_y-I_z}{2}cos2\alpha-I_{yz}sin2\alpha\\ I_z'&=\frac{I_y+I_z}{2}-\frac{I_y-I_z}{2}cos2\alpha+I_{yz}sin2\alpha\\ 有I_y'+I_z'&=I_y+I_z \end{align}\]
\[\begin{align} I_{yz}'=\frac{I_y-I_z}{2}sin2\alpha+I_{yz}cos2\alpha\\ \end{align}\]
- 主惯性轴(Principal axes)令\(I_{yz}=0\)
- 主惯性矩(Principal moment of inertia)
- 形心主惯性轴(centroidal principal axes)
- 形心主惯性矩(centroidal principal moment of inertia) \[\begin{align} tg2\alpha_0&=\frac{-2I_{yz}}{I_{y}-Iz}\\ I_{y.or.z}&=\frac{I_y+I_z}{2}\pm\sqrt{(\frac{I_y-I_z}{2})^2+I_{yz}^2} \end{align}\] > \(I_{y.or.z}\)一个为\(max\)一个\(min\)
应力公式
方向:逆时针转为正
$$\[\begin{align} \sigma_{\alpha}'&=\frac{\sigma_x+\sigma_y}{2}+\frac{\sigma_x-\sigma_y}{2}cos2\alpha-\sigma_{yz}sin2\alpha\\ \end{align}\]$$
\(\sigma_x'+\sigma_y'=\sigma_x+\sigma_y\) 应力不变量
一个点上相互垂直的面的正应力之和是定值
\[\begin{align} \tau_{\alpha}'=\frac{\sigma_x-\sigma_y}{2}sin2\alpha+\tau_{xy}cos2\alpha\\ \end{align}\]
\[\begin{align} tg2\alpha_0&=\frac{-2\tau_{xy}}{\sigma_{y}-\sigma_y}\\ \sigma_{y.or.z}&=\frac{\sigma_x+\sigma_y}{2}\pm\sqrt{(\frac{\sigma_x-\sigma_y}{2})^2+\tau_{xy}^2} \end{align}\] > \(I_{y.or.z}\)一个为\(max\)一个\(min\)
应变公式
方向:逆时针转为正
$$\[\begin{align} \varepsilon_{\alpha}'&=\frac{\varepsilon_x+\varepsilon_y}{2}+\frac{\varepsilon_x-\varepsilon_y}{2}cos2\alpha-\frac{\gamma_{xy}}{2}sin2\alpha\\ \end{align}\]$$
\[\begin{align} \tau_{\alpha}'=\frac{\varepsilon_x-\varepsilon_y}{2}sin2\alpha+\frac{\gamma_{xy}}{2}cos2\alpha\\ \end{align}\]
\[\begin{align} tg2\alpha_0&=\frac{-2\frac{\gamma_{xy}}{2}}{\varepsilon_{y}-\varepsilon_y}\\ \varepsilon_{y.or.z}&=\frac{\varepsilon_x+\varepsilon_y}{2}\pm\sqrt{(\frac{\varepsilon_x-\varepsilon_y}{2})^2+\frac{\gamma_{xy}}{2}^2} \end{align}\]
广义胡克定律
\[\begin{align*} \varepsilon_x&=\frac{1}{E}\left[\sigma_x-\mu(\sigma_y+\sigma_z)\right]\\ \varepsilon_y&=\frac{1}{E}\left[\sigma_y-\mu(\sigma_z+\sigma_x)\right]\\ \varepsilon_z&=\frac{1}{E}\left[\sigma_z-\mu(\sigma_x+\sigma_y)\right] \end{align*}\]
体应变:
\[\begin{align*} \theta&=\varepsilon_x+\varepsilon_y+\varepsilon_z=\frac{1-2\mu}{E}(\sigma_x+\sigma_y+\sigma_z)=\frac{\sigma_m}{K} \\ \text{其中}K&=\frac{E}{3(1-2\mu)} \end{align*}\]
弯曲应力
纯弯曲Pure bending
无剪力只有弯矩
假设
- 平面假设,横截面仍为平面
- 单向受力假设,纵向纤维不相互挤压
\[\begin{align} \varepsilon&=\frac{y}{\rho}\\ \sigma&=E\varepsilon=E\frac{y}{\rho} \end{align}\]
那么中性轴在哪?\(\rho\)是多少?
\(F_N=\int_A E\frac{y}{\rho}dA=0\)\得到中性轴在形心(Centroid of an area)上
立即得\(M_{iy}=\int_A zE\frac{y}{\rho}dA=0\)
\(M_{iz}=\int_A yE\frac{y}{\rho}dA=M\)得到
\[\begin{align} \frac{1}{\rho}=\frac{M}{EI_z}\\ 有\sigma=E\frac{y}{\rho}=\frac{My}{I_z} \end{align}\]
横力弯曲时的正应力(Normal stresses of the beam in nonuniform bending)
\[\begin{align} \sigma&=\frac{M}{W}\\ W&=\frac{I_z}{y_{max}} \end{align}\]
The applicable range of the flexure formula
- All stresses in the beam are below proportional limit
- The beam with the shear stress
- Plane bending
- Straight beams
10.24待补充
弯曲变形(Deflection of beams)
Basic concepts
- Deflection 挠度
- Slope 转角
- Deflection curve 挠曲线
- Relationship between deflection and slope:
\(\theta\approx tan\theta=\omega'\)
- Sign convention for deflection and slope
挠度向上为正
转角自x转至切线,逆时针为正
Differential equation of the deflection curve
\(\frac{1}{\rho}=\frac{M}{EI}\)
\(\frac{1}{\rho}=\frac{\left|\omega''\right|}{(1+\omega'^2)^{\frac{3}{2}}}\)
将\(\omega'^2\)略去
\[\begin{align} EI\omega''=M \end{align}\]
Beam deflection by integration
The first integration gives the equation for the slope;
Integrating again the equation for the deflection.
Evaluating the constants of integration
- Boundary conditions
- Continue conditions
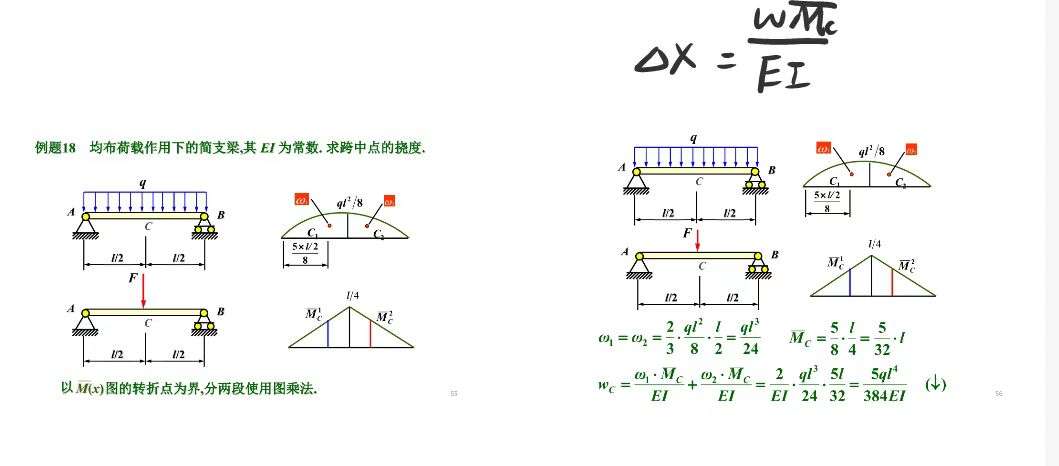
简支梁不管受什么载荷,最大挠度值都可以用中点处值
Superposition
- 载荷叠加(superposition of loads)
- 逐段钢化 有外伸梁时用
经典载荷变形(P195)
能量法
互等定理


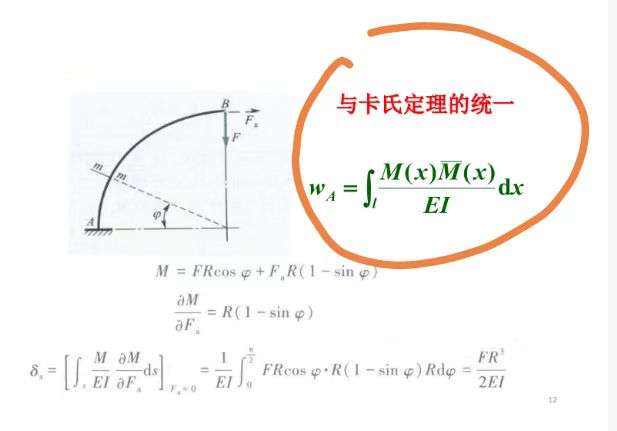
卡氏定理
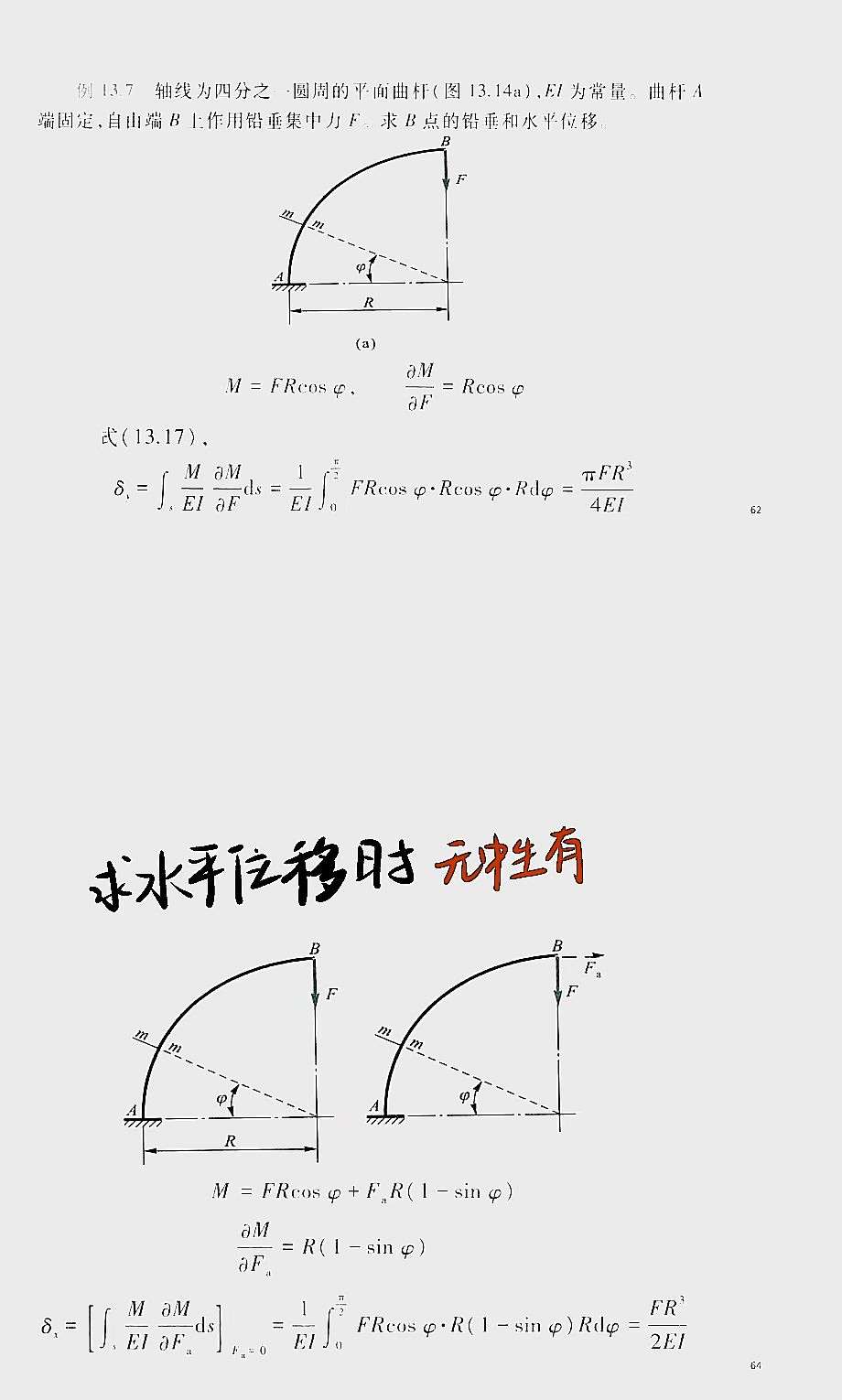
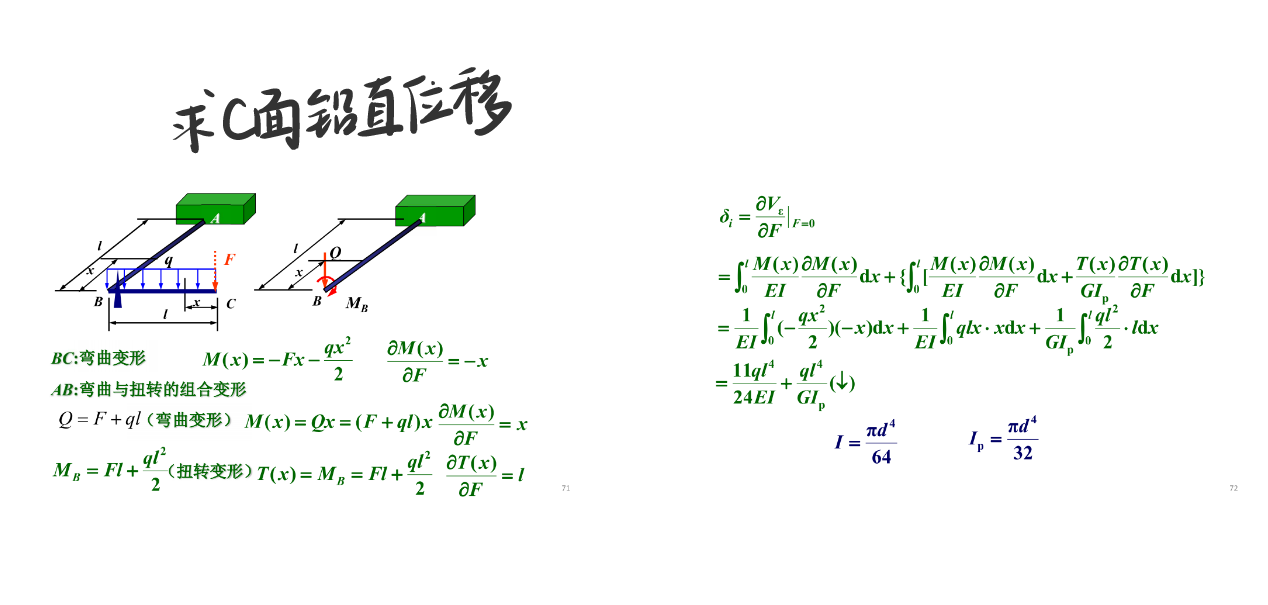
莫尔定理